相关链接
卷积为什么有效?
前面说到在利用基本的神经网络做计算时,会出现参数爆炸的现象,一张 1000*1000*3 的图像,在包含 1000 个隐层的情况下,会有 3 亿个参数需要训练,这无疑是一个很大的问题。那么卷积运算就出现了,因为它的参数真的很少,且很固定。
普通的神经网络计算,权值矩阵 (w) 中的参数的个数是随着输入矩阵的增加而增加的。而在卷积计算中,引入了过滤矩阵(或卷积核),卷积核中的参数的个数,是我们要利用神经网络训练的参数的个数。比如有一个 6*6 的卷积核,那么在本次卷积中,需要确定的参数的个数也就是 36 个。无论是多大的图片,无论图片的大小怎么改变,最终需要确定的只有 36 个参数,这也是神经网络中的一个重要的思想-参数共享。
彩色 (RGB) 图像如何进行卷积计算
前面进行卷积运算时,我们讨论的都是一个简单的二维矩阵,可以认为它是只含有一个通道的图像(黑白图像等),那么彩色图像的卷积应该怎么计算呢?
- 一个
6*6*3的图像,那么为了进行卷积运算,其卷积核也应该是具有三个通道 (channel) 的。这样才能保证计算
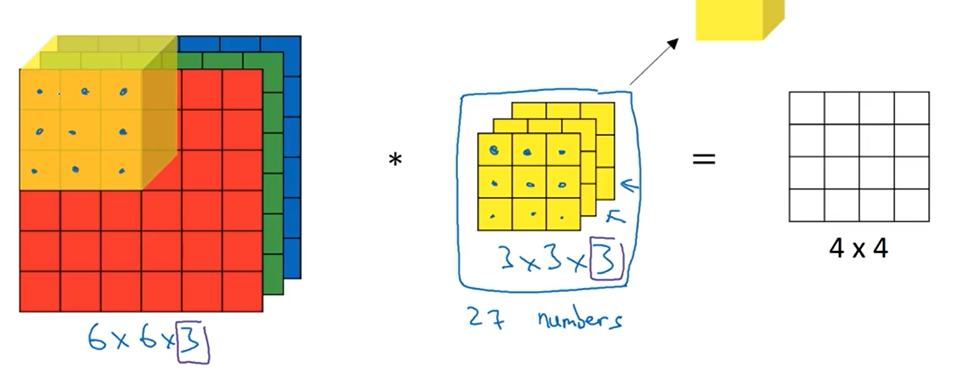
- 计算方法与二维的类似,输入矩阵与过滤矩阵每一层的对应位置的数相乘并相加,最终得到一个数字,也就是做了三次的二维的运算,最终将结果相加起来得到最终的结果。
- 最终输出的结果矩阵,因为只有一个过滤矩阵,所以最终的结果矩阵一定是一个一维的
一定要保证过滤矩阵的通道个数与输入图像的通道个数是相同的,否则无法正确的进行卷积运算。
卷积神经网络中的卷积层是什么?
上面就是基本的卷积计算的运算法则,总结下来一句话:对应位置相乘并相加,算完移位,继续卷积
那根据卷积计算,就可以构造单层卷积网络了,卷积网络与上图的不同是,它是由多个过滤层构成的。
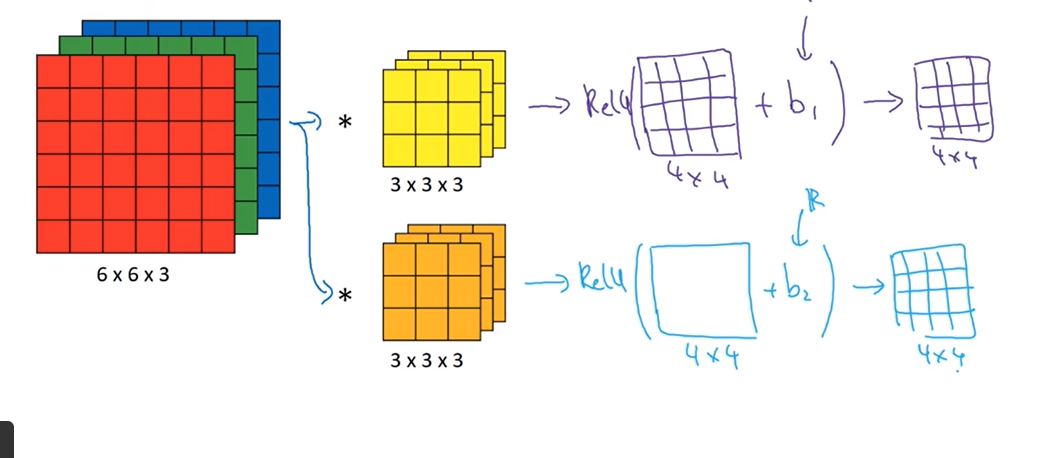
过滤器的作用就是利用不同的卷积核,来提取图像中的某些特征,如
| 1 | 0 | -1 |
|---|---|---|
| 1 | 0 | -1 |
| 1 | 0 | -1 |
就可以用来提取图像中的垂直边界或垂直特征。对图像利用多个过滤器进行卷积运算,将最终的结果组合到一起组成一个新的多维度矩阵,这就是卷积神经网络中的一次卷积运算。
上图中的 6 x 6 x 3 的输入矩阵,分别经过两个 Fliter 进行卷积运算之后,得到两个 4 x 4 x 1 的矩阵,将这两个矩阵组合到一起,也就是最终的 4 x 4 x 2 的输出矩阵,这将作为整个网络下一步操作的输入(卷积,池化等)
基本上到这里就能看懂许多文献上的卷积层了
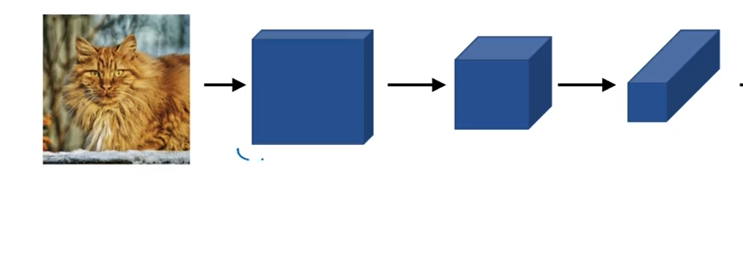
如上图中就是小猫图像,做了三次卷积操作,每次卷积操作的过滤器的数量都会增加,但是过滤器的维度会下降,这是为什么呢?
下一节将介绍
- 卷积神经网络的符号约定
- 池化层
- 全连接层